最大流
问题:我们有一张图,要求从源点流向汇点的最大流量(可以有很多条路到达汇点),就是我们的最大流问题。
Ford-Fulkerson方法
这不是一个完整的算法(因为寻找增广路的方法没有明确),但是下面两个算法的基础。
定义:
- 图 \(G=(V,E)\),源点 \(s\), 汇点 \(t\),\(c(u,v)\)是每条边的容量。
- \(f(u,v)\)是每条边上的当前流值。
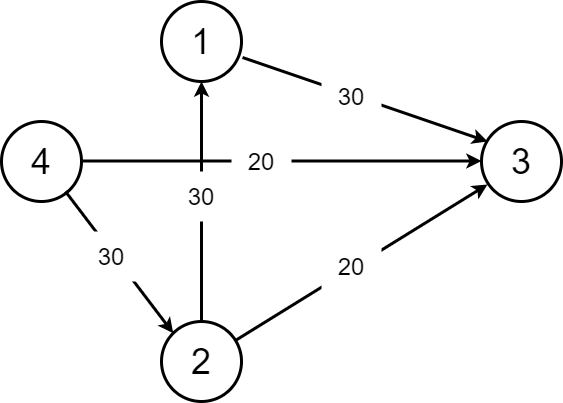
- 增广路:在原图 \(G\) 中若一条从源点到汇点的路径上所有边的 剩余容量都大于 0,这条路被称为增广路(Augmenting Path)。
- 残留图:\(G_f(V, E_f)\),其中每条边的容量为\(c_f(u,v)=c(u,v)-f(u,v)\)。
算法:
- 对所有边\((u,v)\),设\(f(u,v) \leftarrow 0\)
- 当残留图\(G_f\)中有一条从\(s\)到\(t\)的路径\(p\),其上所有边的\(c_f(u,v)>0\)时:
- 找到\(p\)上的残留容量:\(c_f(p)=\min \{c_f(u,v): (u,v)\in p\}\)
- 对于每条边 \((u,v) \in p\)
- \(f(u,v) \leftarrow f(u,v)+c_f(p)\) (修改这边路上的流)
- \(f(v,u) \leftarrow f(v,u)-c_f(p)\) (将来流可以被归还)
复杂度是\(O(Ef)\),\(E\)是边数,\(f\)是最大流。
Edmonds-Karp算法
Edmonds-Karp就是将Ford-Fulkerson的寻找增广路具体化的一个算法,而且使得复杂度降低为多项式时间。算法简单,就是通过BFS找到边数最少的一条增广路径,然后进行增广。
复杂度是\(O(VE^2)\)(\(V\)是点数,\(E\)是边数),比后面的Dinic算法的复杂度要差。实际比赛是用Dinic更合适。
Edmonds-Karp算法
flow := 0 (Initialize flow to zero)
repeat
(Run a breadth-first search (bfs) to find the shortest s-t path.
We use 'pred' to store the edge taken to get to each vertex,
so we can recover the path afterwards)
q := queue()
q.push(s)
pred := array(graph.length)
while not empty(q)
cur := q.pop()
for Edge e in graph[cur] do
if pred[e.t] = null and e.t ≠ s and e.cap > e.flow then
pred[e.t] := e
q.push(e.t)
if not (pred[t] = null) then
(We found an augmenting path.
See how much flow we can send)
df := ∞
for (e := pred[t]; e ≠ null; e := pred[e.s]) do
df := min(df, e.cap - e.flow)
(And update edges by that amount)
for (e := pred[t]; e ≠ null; e := pred[e.s]) do
e.flow := e.flow + df
e.rev.flow := e.rev.flow - df
flow := flow + df
until pred[t] = null (i.e., until no augmenting path was found)
return flow
Dinic算法
每次增广前,使用BFS对图分层,形成一个层次图(Level Graph)。源点层数为0,每个点的层数即为到源点的距离。然后进行增广。
Dinic算法:
- 初始化容量网络和网络流。
- 构造残留网络和层次图,若汇点不在层次网络中,则算法结束。
- 在层次图中用一次DFS过程进行增广(具体步骤见下面代码),找到一个阻塞流(Blocking Flow),DFS执行完毕,该阶段的增广也执行完毕。
- 转步骤2。
相关定义:
- 层次图:\(E_L=\{ (u,v)\in E_f: \operatorname{depth}(v)=\operatorname{depth}(u)+1\}\)
- 阻塞流:指一个源到汇的流\(f'\),使得以下图\(G'\)中没有\(s\)到\(t\)的路径:\(G'=((V,E'_L),s,t), E'_L=\{ (u,v): f'(u,v)<c_f|_{E_L}(u,v) \}\),其中\(c_f|_{E_L}(u,v)\)是层次网络中的边的残留容量。
在Dinic算法中,只需一次DFS过程就可以实现多次增广,这是其巧妙之处。Dinic算法复杂度是\(O(V^2E)\)。
以下实现中,bfs()构造层次网络,dep[]用来记录点的深度。dfs()寻找阻塞流。
// 洛谷P3376:【模板】网络最大流
#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
const int N = 10010, E = 200010;
int n, m, s, t; LL ans = 0;
LL cnt = 1, first[N], nxt[E], to[E], val[E];
inline void addE(int u, int v, LL w) {
to[++cnt] = v;
val[cnt] = w;
nxt[cnt] = first[u];
first[u] = cnt;
}
int dep[N], q[N], l, r;
bool bfs() {//顺着残量网络,方法是 bfs;这是个bool型函数,返回是否搜到了汇点
memset(dep, 0, (n + 1) * sizeof(int));//记得开局先初始化
q[l = r = 1] = s;
dep[s] = 1;
while(l <= r) {
int u = q[l++];
for(int p = first[u]; p; p = nxt[p]) {
int v = to[p];
if(val[p] and !dep[v]) {//按照有残量的边搜过去
dep[v] = dep[u] + 1;
q[++r] = v;
}
}
}
return dep[t];//dep[t] != 0,就是搜到了汇点
}
LL dfs(int u, LL in/*u收到的支持(不一定能真正用掉)*/) {
//注意,return 的是真正输出的流量
if(u == t)
return in;//到达汇点是第一个有效return
LL out = 0;
for(int p = first[u]; p and in; p = nxt[p]) {
int v = to[p];
if(val[p] and dep[v] == dep[u] + 1) {//仅允许流向下一层
LL res = dfs(v, min(val[p], in)/*受一路上最小流量限制*/);
//res是v真正输出到汇点的流量
val[p] -= res;
val[p ^ 1] += res; // val[]成对出现,flip最低bit是另一方向的值
in -= res;
out += res;
}
}
if(out == 0)//我与终点(顺着残量网络)不连通
dep[u] = 0;//上一层的点请别再信任我,别试着给我流量
return out;
}
int main() {
scanf("%d %d %d %d", &n, &m, &s, &t);
for(int i = 1; i <= m; ++i) {
int u, v; LL w;
scanf("%d %d %lld", &u, &v, &w);
addE(u, v, w);
addE(v, u, 0);
}
while(bfs())
ans += dfs(s, 1e18);
printf("%lld\n", ans);
return 0;
}
Wikipedia有一个完整的例子。